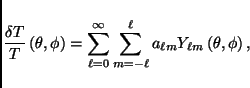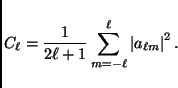Next: Recent results
Up: Introduction
Previous: Introduction
In the framework of Big-Bang theory, the Universe started with a hot
and dense phase about 15 billion years ago and cooled down while
expanding. The first neutral atoms formed when the temperature was
about 13.6 eV (160000 K), but due to the large number of photons
compared to baryons (ratio 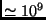 ), the Universe remained
ionized until the temperature dropped below 0.3 eV (3000 K). At this
moment, the mean free path of the photons increased drastically so
that the photons that scattered at this time have not interacted with
matter since then. This moment is known as matter-radiation
decoupling or recombination. Those photons cooled down with
the expansion of the Universe and are know observed at a temperature
of 2.7 K. As the matter and radiation were at thermal equilibrium
before decoupling, these photons have a pure blackbody spectrum and
are homogeneously distributed on the celestial sphere. This radiation
is known as the Cosmic Microwave Background (hereafter CMB).
), the Universe remained
ionized until the temperature dropped below 0.3 eV (3000 K). At this
moment, the mean free path of the photons increased drastically so
that the photons that scattered at this time have not interacted with
matter since then. This moment is known as matter-radiation
decoupling or recombination. Those photons cooled down with
the expansion of the Universe and are know observed at a temperature
of 2.7 K. As the matter and radiation were at thermal equilibrium
before decoupling, these photons have a pure blackbody spectrum and
are homogeneously distributed on the celestial sphere. This radiation
is known as the Cosmic Microwave Background (hereafter CMB).
The discovery of the CMB by Penzias and Wilson [1]
and its interpretation in terms of a Big-Bang relic by Dicke and
collaborators [2] was a major argument for the Big-Bang
theory [3,4]. The CMB temperature was measured to
be highly isotropic but tiny anisotropies were expected. These
temperature fluctuations reflect the density fluctuations on the last
scattering surface. These are necessary to explain the presence of
structures in the Universe such as galaxies and clusters. The CMB
anisotropies were discovered by the COBE satellite with a rms
amplitude of about 30 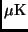 [5] at scales larger
than 7 degrees. COBE also measured its spectrum with high
precision [6,7] proving its pure blackbody nature.
[5] at scales larger
than 7 degrees. COBE also measured its spectrum with high
precision [6,7] proving its pure blackbody nature.
The CMB anisotropy typical physical size in the last scattering
surface can be theoretically predicted while its angular size as seen
from here and now depends on the geometry of the Universe along the
path of the photons. Hence, mapping the CMB anisotropies is a powerful
cosmological test.
The two competing paradigms for the origin of structures in the
Universe, namely inflation and topological defects, predict
significantly different distributions for the former density
fluctuations. These distributions propagate to us in a cosmological
parameters dependent way to describe the temperature anisotropies that
we expect on the sky1.
It is therefore of deep interest to investigate their angular
distribution and compare the measurements to cosmological models.
The temperature anisotropies on the sky are commonly described via their spherical harmonics expansion,
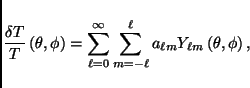 |
(1) |
where 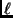 is the multipole index, inversely proportional to the
angular scale (1 degree roughly corresponds to
is the multipole index, inversely proportional to the
angular scale (1 degree roughly corresponds to 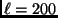 ). The angular power spectrum of the temperature fluctuations of the CMB is defined as:
). The angular power spectrum of the temperature fluctuations of the CMB is defined as:
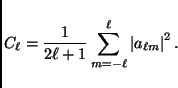 |
(2) |
The evolution of the angular power spectrum of the CMB as a function of 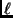 can be splitted into three major regions (see Figure
can be splitted into three major regions (see Figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
- On the low-
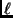 part (large angular scales) no particular
structure is expected as we are considering physical sizes on the
last scattering surface larger than the horizon at the epoch of
decoupling. No physical process is expected to have modified those
fluctuations since the early Universe.
part (large angular scales) no particular
structure is expected as we are considering physical sizes on the
last scattering surface larger than the horizon at the epoch of
decoupling. No physical process is expected to have modified those
fluctuations since the early Universe.
- Between
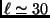 and
and
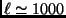 (degree and
sub-degree scales) we a re considering structures that had time to
collapse and experience acoustic oscillations between the
matter-radiation equality and the matter radiation decoupling. We
therefore expect a series of acoustic peaks (the first one being
located around
(degree and
sub-degree scales) we a re considering structures that had time to
collapse and experience acoustic oscillations between the
matter-radiation equality and the matter radiation decoupling. We
therefore expect a series of acoustic peaks (the first one being
located around 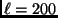 , corresponding to the size of the horizon
at the epoch of decoupling) in the case of inflationary-like early
Universe models where the oscillations are in phase. In the case of
isocurvature fluctuations (such as topological defects), the
oscillations are not in phase and a large bump is expected, but no
multiple peaks.
, corresponding to the size of the horizon
at the epoch of decoupling) in the case of inflationary-like early
Universe models where the oscillations are in phase. In the case of
isocurvature fluctuations (such as topological defects), the
oscillations are not in phase and a large bump is expected, but no
multiple peaks.
- In the large
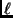 part (arcminute scales and below), the power
is expected to drop drastically due to the finite thickness of the
last scattering surface and to the finite value of the mean free
path of the photons before decoupling.
part (arcminute scales and below), the power
is expected to drop drastically due to the finite thickness of the
last scattering surface and to the finite value of the mean free
path of the photons before decoupling.
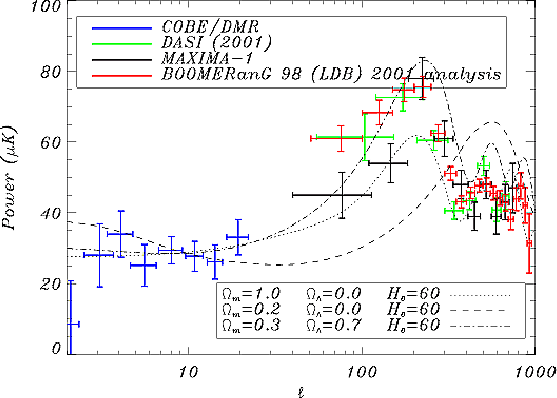
Figure:
Expected CMB power spectrum
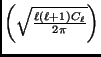 for
inflationary-like primordial density fluctuations (black curves) for
three different cosmological models along with the latest
measurements from BOOMERanG, MAXIMA and DASI and the earlier
measurements from COBE.
for
inflationary-like primordial density fluctuations (black curves) for
three different cosmological models along with the latest
measurements from BOOMERanG, MAXIMA and DASI and the earlier
measurements from COBE.
 |



Next: Recent results
Up: Introduction
Previous: Introduction
Jean-Christophe Hamilton ISN
2001-12-01
![]() [5] at scales larger
than 7 degrees. COBE also measured its spectrum with high
precision [6,7] proving its pure blackbody nature.
[5] at scales larger
than 7 degrees. COBE also measured its spectrum with high
precision [6,7] proving its pure blackbody nature.