


Next: Perspectives for incoming flights
Up: Data analysis
Previous: Calibration
We use the MASTER method [19] in order to measure the power
spectrum on our maps. Within this framework, maps are obtained by
coadding the filtered timelines on the sky. In the case of pure white
noise, this leads to optimal maps. We filter our timelines keeping
only frequencies between 1 and 45 Hz so that the resulting power
spectrum is very close to be white. The pseudo- spectrum is
obtained using anafast in Healpix package [20]. We then
estimate the noise angular power spectrum on the coadded maps using a
set of Monte-Carlo simulations. The effect of the filter on the
underlying sky is also estimated via Monte-Carlo simulations. The mode
mixing effect is deconvolved following [19]. All these
corrections allow us to transform the pseudo-
spectrum is
obtained using anafast in Healpix package [20]. We then
estimate the noise angular power spectrum on the coadded maps using a
set of Monte-Carlo simulations. The effect of the filter on the
underlying sky is also estimated via Monte-Carlo simulations. The mode
mixing effect is deconvolved following [19]. All these
corrections allow us to transform the pseudo- spectrum into a
real angular power spectrum. We estimated the non optimality of our
power spectrum (due to the non optimal maps) to be less than 30% at
all scales. The power spectrum estimation is at the moment under test.
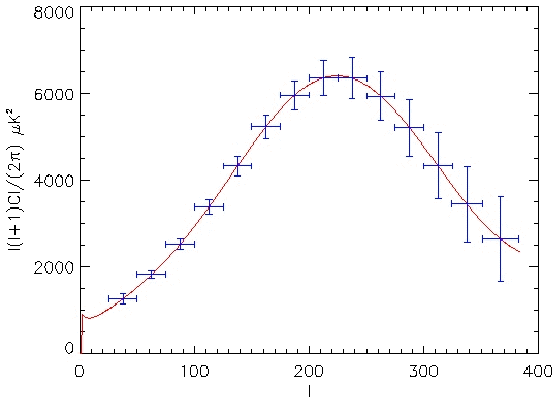
The expected accuracy for 10 bolometers, obtained through full simulations from
timelines to power spectrum with realistic noise (measured on the real
timelines), is shown in top panel of Figure
spectrum into a
real angular power spectrum. We estimated the non optimality of our
power spectrum (due to the non optimal maps) to be less than 30% at
all scales. The power spectrum estimation is at the moment under test.
The expected accuracy for 10 bolometers, obtained through full simulations from
timelines to power spectrum with realistic noise (measured on the real
timelines), is shown in top panel of Figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
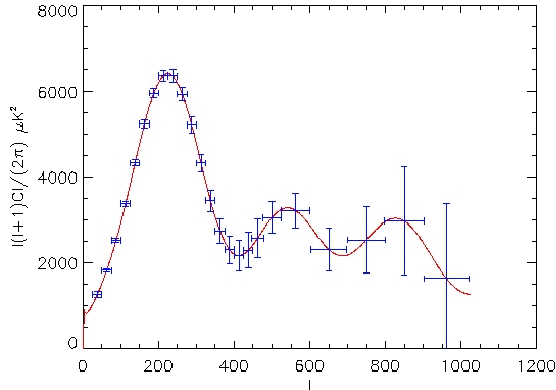
Figure:
Estimated power spectrum accuracy for the 7h30 Kiruna scientific
flight (top) and for the incoming 24 hours flights (bottom). Both
were obtained for 10 bolometers from the average of one thousand
realistic simulations of the Archeops timelines and noise
structure.
 |



Next: Perspectives for incoming flights
Up: Data analysis
Previous: Calibration
Jean-Christophe Hamilton ISN
2001-12-01



